Stata Create Categorical Variable From Continuous
This page is archived and no longer maintained.
This is a draft version of this chapter. Comments and suggestions to improve this draft are welcome.
Chapter Outline
1. Continuous and Categorical Predictors without Interaction
2. Continuous and Categorical Predictors with Interaction
3. Show slopes for each group
3.1 Show slopes by performing separate analyses
3.2 Show slopes for each group from one analysis
4. Compare slopes across groups
5. Simple effects and simple comparisons of group, strategy 1
5.1 Simple effects and comparisons when meals is 1 sd below mean
5.2 Simple effects and comparisons when meals is at the mean
5.3 Simple effects and comparisons when meals is 1 sd above the mean
6. Simple effects and simple comparisons of group, strategy 2
6.1 Simple effects and comparisons when meals is 1 sd below mean
6.2 Simple effects and comparisons when meals is at the mean
6.3 Simple effects and comparisons when meals is 1 sd above mean
7. Interaction Comparison
8. More on predicted values
Please note: This page makes use of the programs xi3 and postgr3 which are no longer being maintained and has been removed from our archives. References to xi3 and postgr3 will be left on this page because they illustrate specific principles of coding categorical variables.
In this chapter we continue to use the elemapi2 data file which we can use as shown below.
use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/elemapi2, clear
1. Continuous and Categorical Predictors without Interaction
In this model we have collcat as a categorical variable with 3 levels and meals as continuous variable. We will use reverse Helmert coding for collcat which will be useful for later analyses.
This uses the xi3 command.
xi3: regress api00 r.collcat meals
r.collcat _Icollcat_1-3 (naturally coded; _Icollcat_1 omitted) Source | SS df MS Number of obs = 400 -------------+------------------------------ F( 3, 396) = 584.83 Model | 6586951.80 3 2195650.60 Prob > F = 0.0000 Residual | 1486720.20 396 3754.34394 R-squared = 0.8159 -------------+------------------------------ Adj R-squared = 0.8145 Total | 8073672.00 399 20234.7669 Root MSE = 61.273 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- _Icollcat_2 | 14.01454 7.627863 1.84 0.067 -.981627 29.01071 _Icollcat_3 | 17.23322 6.581453 2.62 0.009 4.294266 30.17218 meals | -3.942667 .0988327 -39.89 0.000 -4.13697 -3.748365 _cons | 885.1789 6.718856 131.75 0.000 871.9698 898.388 ------------------------------------------------------------------------------
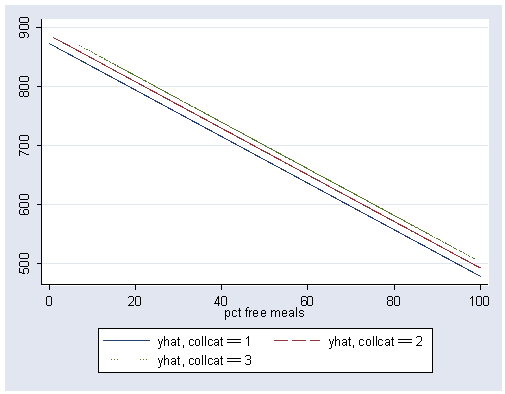
If we look at the predicted values, we can see that there are 3 regression lines, each of which are parallel. We graph the predicted values below.
predict yhat
(option xb assumed; fitted values)
separate yhat , by(collcat)
storage display value variable name type format label variable label ------------------------------------------------------------------------------- yhat1 float %9.0g yhat, collcat == 1 yhat2 float %9.0g yhat, collcat == 2 yhat3 float %9.0g yhat, collcat == 3
graph twoway scatter yhat1 yhat2 yhat3 meals, connect(l l l) clpattern(solid longdash dot) msymbol(i i i)
We drop the variables yhat yhat1 yhat2 yhat3 in case we want to use them later.
drop yhat yhat1 yhat2 yhat3
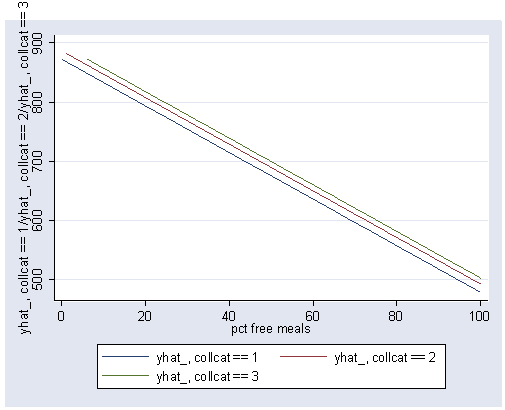
We could also get these results using the postgr3 command.
postgr3 meals, by(collcat)
Variables left asis: meals _Icollcat_2 _Icollcat_3 (option xb assumed; fitted values)
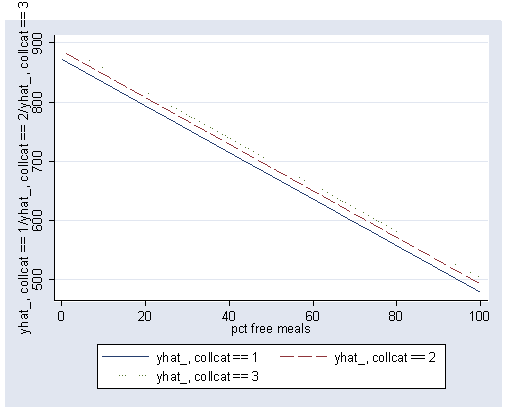
If you wanted to indicate the different groups using different types of lines we could use the clpattern option.
postgr3 meals, by(collcat) clpattern(solid longdash dot)
Variables left asis: meals _Icollcat_2 _Icollcat_3 (option xb assumed; fitted values)
2. Continuous and Categorical Predictors with Interaction
The prior analysis assumed that the slopes for the 3 collcat groups are the same. We can test this assumption by including an interaction of collcat by meals.
xi3: regress api00 r.collcat*meals
r.collcat _Icollcat_1-3 (naturally coded; _Icollcat_1 omitted) Source | SS df MS Number of obs = 400 -------------+------------------------------ F( 5, 394) = 361.86 Model | 6629929.87 5 1325985.97 Prob > F = 0.0000 Residual | 1443742.12 394 3664.32011 R-squared = 0.8212 -------------+------------------------------ Adj R-squared = 0.8189 Total | 8073672 399 20234.7669 Root MSE = 60.534 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- _Icollcat_2 | 10.29492 16.24717 0.63 0.527 -21.64707 42.23691 _Icollcat_3 | -26.4292 14.31193 -1.85 0.066 -54.5665 1.708093 meals | -3.859353 .1006356 -38.35 0.000 -4.057203 -3.661503 _Ico2Xme | .0281506 .2225014 0.13 0.899 -.4092879 .4655891 _Ico3Xme | .7948911 .2324169 3.42 0.001 .3379588 1.251823 _cons | 882.4703 6.690036 131.91 0.000 869.3176 895.6229 ------------------------------------------------------------------------------
We can then test overall interaction and we see that the interaction is significant.
test _Ico2Xme _Ico3Xme
( 1) _Ico2Xme = 0.0 ( 2) _Ico3Xme = 0.0 F( 2, 394) = 5.86 Prob > F = 0.0031
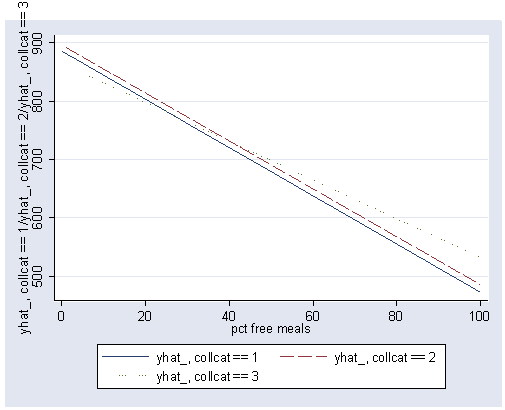
Again we use the postgr3 command to show the graph of the regression lines between meals and api00 for the 3 levels of collcat and we see that the lines are not parallel (as we would expect because of the significant interaction we found above).
postgr3 meals, by(collcat) clpattern(solid longdash dot)
Variables left asis: meals _Icollcat_2 _Icollcat_3 _Ico2Xme _Ico3Xme (option xb assumed; fitted values)
3. Show slopes for each group
3.1 Show slopes by performing separate analyses
We can perform separate analyses by collcat to get slope of meals at each level of collcat.
bysort collcat : regress api00 meals
_______________________________________________________________________________ -> collcat = 1 Source | SS df MS Number of obs = 129 -------------+------------------------------ F( 1, 127) = 664.41 Model | 2617392.53 1 2617392.53 Prob > F = 0.0000 Residual | 500306.775 127 3939.42342 R-squared = 0.8395 -------------+------------------------------ Adj R-squared = 0.8383 Total | 3117699.30 128 24357.0258 Root MSE = 62.765 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- meals | -4.138392 .1605512 -25.78 0.000 -4.456094 -3.82069 _cons | 886.1325 12.52709 70.74 0.000 861.3437 910.9214 ------------------------------------------------------------------------------ _______________________________________________________________________________ -> collcat = 2 Source | SS df MS Number of obs = 134 -------------+------------------------------ F( 1, 132) = 676.61 Model | 2424781.52 1 2424781.52 Prob > F = 0.0000 Residual | 473049.976 132 3583.71194 R-squared = 0.8368 -------------+------------------------------ Adj R-squared = 0.8355 Total | 2897831.50 133 21788.2068 Root MSE = 59.864 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- meals | -4.110242 .1580147 -26.01 0.000 -4.42281 -3.797673 _cons | 896.4275 10.7427 83.45 0.000 875.1773 917.6776 ------------------------------------------------------------------------------ _______________________________________________________________________________ -> collcat = 3 Source | SS df MS Number of obs = 137 -------------+------------------------------ F( 1, 135) = 279.96 Model | 975465.983 1 975465.983 Prob > F = 0.0000 Residual | 470385.375 135 3484.33611 R-squared = 0.6747 -------------+------------------------------ Adj R-squared = 0.6723 Total | 1445851.36 136 10631.26 Root MSE = 59.028 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- meals | -3.329426 .1989864 -16.73 0.000 -3.72296 -2.935892 _cons | 864.8508 11.48996 75.27 0.000 842.1272 887.5744 ------------------------------------------------------------------------------
3.2 Show slopes for each group in one analysis
We can also get the slope of meals at each level of collcat via one overall regression. One way is to dummy code the categorical variable collcat and to create interaction terms with variable meals. The trick is to include all the interaction terms, leaving out both meals and one of the categories of collcat out of the regression. Then the coefficient for each of the interaction terms will be the slope of meals for each group of collcat. In our case, the slope of meals for group 1 of collcat is -4.138392, -4.110242 for group 2 and -3.329426 for group 3 as shown in the regression output below.
tab collcat, gen(cd)
collcat | Freq. Percent Cum. ------------+----------------------------------- 1 | 129 32.25 32.25 2 | 134 33.50 65.75 3 | 137 34.25 100.00 ------------+----------------------------------- Total | 400 100.00
gen cdm1 = cd1*meals gen cdm2 = cd2*meals gen cdm3 = cd3*meals
. regress api00 cd1 cd2 cdm1 cdm2 cdm3
Source | SS df MS Number of obs = 400 -------------+------------------------------ F( 5, 394) = 361.86 Model | 6629929.87 5 1325985.97 Prob > F = 0.0000 Residual | 1443742.13 394 3664.32012 R-squared = 0.8212 -------------+------------------------------ Adj R-squared = 0.8189 Total | 8073672.00 399 20234.7669 Root MSE = 60.534
------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- cd1 | 21.28174 16.87625 1.26 0.208 -11.89701 54.46049 cd2 | 31.57666 16.02623 1.97 0.050 .06904 63.08428 cdm1 | -4.138392 .1548438 -26.73 0.000 -4.442816 -3.833969 cdm2 | -4.110242 .159782 -25.72 0.000 -4.424373 -3.79611 cdm3 | -3.329426 .204061 -16.32 0.000 -3.73061 -2.928241 _cons | 864.8508 11.78298 73.40 0.000 841.6854 888.0162 ------------------------------------------------------------------------------
4. Compare slopes across groups
Compare slopes 3 vs. 1 and 2, 2 vs 1.
xi3: regress api00 r.collcat*meals
r.collcat _Icollcat_1-3 (naturally coded; _Icollcat_1 omitted) Source | SS df MS Number of obs = 400 -------------+------------------------------ F( 5, 394) = 361.86 Model | 6629929.87 5 1325985.97 Prob > F = 0.0000 Residual | 1443742.12 394 3664.32011 R-squared = 0.8212 -------------+------------------------------ Adj R-squared = 0.8189 Total | 8073672 399 20234.7669 Root MSE = 60.534 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- _Icollcat_2 | 10.29492 16.24717 0.63 0.527 -21.64707 42.23691 _Icollcat_3 | -26.4292 14.31193 -1.85 0.066 -54.5665 1.708093 meals | -3.859353 .1006356 -38.35 0.000 -4.057203 -3.661503 _Ico2Xme | .0281506 .2225014 0.13 0.899 -.4092879 .4655891 _Ico3Xme | .7948911 .2324169 3.42 0.001 .3379588 1.251823 _cons | 882.4703 6.690036 131.91 0.000 869.3176 895.6229 ------------------------------------------------------------------------------
desc _Ico2Xme _Ico3Xme
storage display value variable name type format label variable label ------------------------------------------------------------------------------- _Ico2Xme float %9.0g collcat(2 vs. 1)*meals _Ico3Xme float %9.0g collcat(3 vs. 2-)*meals
slopes 1 and 2 do not differ, but 1 and 2 vs. 3 differ.
5. Simple effects and simple comparisons of group, strategy 1
Test simple effects and simple comparisons of collcat at meals mean-1sd, mean, mean+1sd get mean-1sd, mean, mean+1sd
summarize meals
Variable | Obs Mean Std. Dev. Min Max -------------+----------------------------------------------------- meals | 400 60.315 31.9117 0 100
show graph with lines at each level for simple effect we will test effect of collcat at the 3 places where the vertical lines are drawn in the graph.
postgr3 meals, by(collcat) clpattern(solid longdash dot) xline(28.4033 60.315 92.2267)
Variables left asis: meals _Icollcat_2 _Icollcat_3 _IcolXmeals_2 _IcolXmeals_3 (option xb assumed; fitted values)
5.1 Simple effects and comparisons when meals is 1 sd below mean
generate mealslow = meals-28.4033
. xi3: regress api00 r.collcat*mealslow
r.collcat _Icollcat_1-3 (naturally coded; _Icollcat_1 omitted) Source | SS df MS Number of obs = 400 -------------+------------------------------ F( 5, 394) = 361.86 Model | 6629929.86 5 1325985.97 Prob > F = 0.0000 Residual | 1443742.14 394 3664.32015 R-squared = 0.8212 -------------+------------------------------ Adj R-squared = 0.8189 Total | 8073672 399 20234.7669 Root MSE = 60.534 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- _Icollcat_2 | 11.09449 11.05054 1.00 0.316 -10.63089 32.81988 _Icollcat_3 | -3.85167 8.95725 -0.43 0.667 -21.46165 13.75831 mealslow | -3.859353 .1006356 -38.35 0.000 -4.057203 -3.661503 _Ico2Xme | .0281505 .2225014 0.13 0.899 -.409288 .4655891 _Ico3Xme | .794891 .2324169 3.42 0.001 .3379587 1.251823 _cons | 772.8519 4.369313 176.88 0.000 764.2618 781.442 ------------------------------------------------------------------------------
Below we show the simple effect of collcat when meals is one standard deviation below the mean (i.e. when meals is 28.4033).
test _Icollcat_2 _Icollcat_3
( 1) _Icollcat_2 = 0.0 ( 2) _Icollcat_3 = 0.0 F( 2, 394) = 0.64 Prob > F = 0.5277
If we want a simple comparison of 2 vs 1 at 28.4 we can simply inspect the test for _Icollcat_2 since this compares levels 2 and 1 of collcat.
We can obtain predicted values for when collcat is 1 and 2 at meals=28.4 as shown below.
lincom _cons + -.5*_Icollcat_2 + -.333333*_Icollcat_3
( 1) - .5 _Icollcat_2 - .333333 _Icollcat_3 + _cons = 0.0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | 768.5885 8.362915 91.90 0.000 752.147 785.0301 ------------------------------------------------------------------------------
lincom _cons + .5*_Icollcat_2 + -.333333*_Icollcat_3
( 1) .5 _Icollcat_2 - .333333 _Icollcat_3 + _cons = 0.0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | 779.683 7.223292 107.94 0.000 765.482 793.884 ------------------------------------------------------------------------------
We can obtain the simple comparison that compares level 3 of collcat vs levels 1 and 2 combined when meals is 28.4 by inspecting the coefficient for _Icollcat_3. We can obtain predicted values for levels 1 and 2 of collcat combined and for level 3 of collcat when meals=28.4 as shown below.
lincom _cons + 0*_Icollcat_2 + -.333333*_Icollcat_3
( 1) - .333333 _Icollcat_3 + _cons = 0.0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | 774.1358 5.525266 140.11 0.000 763.2731 784.9985 ------------------------------------------------------------------------------
lincom _cons + 0*_Icollcat_2 + .666667*_Icollcat_3
( 1) .666667 _Icollcat_3 + _cons = 0.0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | 770.2841 7.050091 109.26 0.000 756.4236 784.1446 ------------------------------------------------------------------------------
5.2 Simple effects and comparisons when meals is at the mean
We can obtain simple effects and simple comparisons of collcat when meals is at the mean much like we did above, as shown below.
generate mealsmn = meals-(60.315)
. xi3: regress api00 r.collcat*mealsmn
r.collcat _Icollcat_1-3 (naturally coded; _Icollcat_1 omitted) Source | SS df MS Number of obs = 400 -------------+------------------------------ F( 5, 394) = 361.86 Model | 6629929.87 5 1325985.97 Prob > F = 0.0000 Residual | 1443742.12 394 3664.32011 R-squared = 0.8212 -------------+------------------------------ Adj R-squared = 0.8189 Total | 8073672 399 20234.7669 Root MSE = 60.534 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- _Icollcat_2 | 11.99283 7.617381 1.57 0.116 -2.982969 26.96862 _Icollcat_3 | 21.51465 6.649319 3.24 0.001 8.44207 34.58724 mealsmn | -3.859353 .1006356 -38.35 0.000 -4.057203 -3.661503 _Ico2Xme | .0281506 .2225014 0.13 0.899 -.409288 .4655891 _Ico3Xme | .7948911 .2324169 3.42 0.001 .3379587 1.251823 _cons | 649.6934 3.122175 208.09 0.000 643.5552 655.8316 ------------------------------------------------------------------------------
simple effect of collcat at meals=mean
test _Icollcat_2 _Icollcat_3
( 1) _Icollcat_2 = 0.0 ( 2) _Icollcat_3 = 0.0 F( 2, 394) = 6.31 Prob > F = 0.0020
The simple comparison of 2 vs 1 at when meals is 60.3 can be seen in the test of _Icollcat_2 and the simple comparison of 3 vs 2 and 1 when meals is 60.3 can be seen in the test of _Icollcat_3.
5.3 Simple effects and comparisons when meals is 1 sd above the mean
The simple effects and simple comparisons of collcat when meals is one standard deviation above the mean (i.e. 60.315+ 31.9117) is illustrated below.
generate mealshi = meals - 92.2267
. xi3: regress api00 r.collcat*mealshi
r.collcat _Icollcat_1-3 (naturally coded; _Icollcat_1 omitted) Source | SS df MS Number of obs = 400 -------------+------------------------------ F( 5, 394) = 361.86 Model | 6629929.87 5 1325985.97 Prob > F = 0.0000 Residual | 1443742.13 394 3664.32012 R-squared = 0.8212 -------------+------------------------------ Adj R-squared = 0.8189 Total | 8073672 399 20234.7669 Root MSE = 60.534 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- _Icollcat_2 | 12.89116 9.734782 1.32 0.186 -6.247452 32.02977 _Icollcat_3 | 46.88098 10.87258 4.31 0.000 25.50546 68.2565 mealshi | -3.859353 .1006356 -38.35 0.000 -4.057203 -3.661503 _Ico2Xme | .0281506 .2225014 0.13 0.899 -.4092879 .4655891 _Ico3Xme | .7948911 .2324169 3.42 0.001 .3379587 1.251823 _cons | 526.5349 4.586059 114.81 0.000 517.5186 535.5511 ------------------------------------------------------------------------------
simple effects of collcat when meals = mean + 1sd
test _Icollcat_2 _Icollcat_3
( 1) _Icollcat_2 = 0.0 ( 2) _Icollcat_3 = 0.0 F( 2, 394) = 10.61 Prob > F = 0.0000
The simple comparison of 2 vs. 1 at when meals is 92.22 can be seen in the test of _Icollcat_2 and the simple comparison of 3 vs. 2 and 1 when meals is 92.22 can be seen in the test of _Icollcat_3.
6. Simple effects and simple comparisons of group, strategy 2
This strategy shows how to do these same comparisons all via one model.
xi3: regress api00 r.collcat*meals
r.collcat _Icollcat_1-3 (naturally coded; _Icollcat_1 omitted) Source | SS df MS Number of obs = 400 -------------+------------------------------ F( 5, 394) = 361.86 Model | 6629929.87 5 1325985.97 Prob > F = 0.0000 Residual | 1443742.12 394 3664.32011 R-squared = 0.8212 -------------+------------------------------ Adj R-squared = 0.8189 Total | 8073672 399 20234.7669 Root MSE = 60.534 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- _Icollcat_2 | 10.29492 16.24717 0.63 0.527 -21.64707 42.23691 _Icollcat_3 | -26.4292 14.31193 -1.85 0.066 -54.5665 1.708093 meals | -3.859353 .1006356 -38.35 0.000 -4.057203 -3.661503 _Ico2Xme | .0281506 .2225014 0.13 0.899 -.4092879 .4655891 _Ico3Xme | .7948911 .2324169 3.42 0.001 .3379588 1.251823 _cons | 882.4703 6.690036 131.91 0.000 869.3176 895.6229 ------------------------------------------------------------------------------
6.1 Simple effects and comparisons when meals is 1 sd below mean
test simple effect of collcat when meals is one standard deviation below the mean, i.e. 28.403.
test _Icollcat_2+ 28.403*_Ico2Xme =0
( 1) _Icollcat_2 + 28.403 _Ico2Xme = 0.0 F( 1, 394) = 1.01 Prob > F = 0.3160
test _Icollcat_3+ 28.403*_Ico3Xme =0, accum
( 1) _Icollcat_2 + 28.403 _Ico2Xme = 0.0 ( 2) _Icollcat_3 + 28.403 _Ico3Xme = 0.0 F( 2, 394) = 0.64 Prob > F = 0.5277
Compare collcat groups 2 vs. 1 when meals is at 28.403.
lincom _Icollcat_2+ 28.403*_Ico2Xme
( 1) _Icollcat_2 + 28.403 _Ico2Xme = 0.0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | 11.09449 11.05058 1.00 0.316 -10.631 32.81997 ------------------------------------------------------------------------------
obtain predicted values for collcat groups 1 and 2 when meals is 28.403.
lincom _cons + -.5*_Icollcat_2 + -.333333*_Icollcat_3 + 28.403*meals + /// (-.5*28.403)*_Ico2Xme + (-.333333*28.403)*_Ico3Xme
( 1) - .5 _Icollcat_2 - .333333 _Icollcat_3 + 28.403 meals - 14.2015 _Ico2Xme - 9.467657 _Ico3Xme + _cons = 0.0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | 768.5898 8.362951 91.90 0.000 752.1482 785.0314 ------------------------------------------------------------------------------
lincom _cons + .5*_Icollcat_2 + -.333333*_Icollcat_3 + 28.403*meals + /// ( .5*28.403)*_Ico2Xme + (-.333333*28.403)*_Ico3Xme
( 1) .5 _Icollcat_2 - .333333 _Icollcat_3 + 28.403 meals + 14.2015 _Ico2Xme - 9.467657 _Ico3Xme + _cons = 0.0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | 779.6843 7.223325 107.94 0.000 765.4832 793.8853 ------------------------------------------------------------------------------
test simple comparison when mean-1sd, 1 and 2 vs 3.
lincom _Icollcat_3 + 28.403*_Ico3Xme
( 1) _Icollcat_3 + 28.403 _Ico3Xme = 0.0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | -3.851909 8.957298 -0.43 0.667 -21.46198 13.75817 ------------------------------------------------------------------------------
obtain predicted values for groups 1 and 2 vs 3.
lincom _cons + 0*_Icollcat_2 + -.333333*_Icollcat_3 + 28.403*meals + /// (0*28.403)*_Ico2Xme + (-.333333*28.403)*_Ico3Xme
( 1) - .333333 _Icollcat_3 + 28.403 meals - 9.467657 _IcolXmeals_3 + _cons = 0.0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | 774.137 5.52529 140.11 0.000 763.2743 784.9998 ------------------------------------------------------------------------------
lincom _cons + 0*_Icollcat_2 + .666667*_Icollcat_3 + 28.403*meals + /// (0*28.403)*_Ico2Xme + ( .666667*28.403)*_Ico3Xme
( 1) .666667 _Icollcat_3 + 28.403 meals + 18.93534 _Ico3Xme + _cons = 0.0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | 770.2851 7.050132 109.26 0.000 756.4245 784.1457 ------------------------------------------------------------------------------
6.2 Simple effects and comparisons when meals is at the mean
test simple effect when meals = mean
test _Icollcat_2+ 60.315*_Ico2Xme =0
( 1) _Icollcat_2 + 60.315 _Ico2Xme = 0.0 F( 1, 394) = 2.48 Prob > F = 0.1162
test _Icollcat_3+ 60.315*_Ico3Xme =0, accum
( 1) _Icollcat_2 + 60.315 _Ico2Xme = 0.0 ( 2) _Icollcat_3 + 60.315 _Ico3Xme = 0.0 F( 2, 394) = 6.31 Prob > F = 0.0020
test simple comparison 2 vs. 1.
lincom _Icollcat_2+ 60.315*_Ico2Xme
( 1) _Icollcat_2 + 60.315 _Ico2Xme = 0.0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | 11.99283 7.617381 1.57 0.116 -2.982967 26.96862 ------------------------------------------------------------------------------
test simple comparison 1 and 2 vs. 3
lincom _Icollcat_3+ 60.315*_Ico3Xme
( 1) _Icollcat_3 + 60.315 _Ico3Xme = 0.0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | 21.51465 6.649319 3.24 0.001 8.442072 34.58724 ------------------------------------------------------------------------------
6.3 Simple effects and comparisons when meals is 1 sd above mean
test simple effect when mean+1sd
test _Icollcat_2+ 92.23*_Ico2Xme =0
( 1) _Icollcat_2 + 92.23 _Ico2Xme = 0.0 F( 1, 394) = 1.75 Prob > F = 0.1862
test _Icollcat_3+ 92.23*_Ico3Xme =0, accum
( 1) _Icollcat_2 + 92.23 _Ico2Xme = 0.0 ( 2) _Icollcat_3 + 92.23 _Ico3Xme = 0.0 F( 2, 394) = 10.61 Prob > F = 0.0000
test simple comparison 2 vs. 1
lincom _Icollcat_2+ 92.23*_Ico2Xme
( 1) _Icollcat_2 + 92.23 _IcolXmeals_2 = 0.0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | 12.89125 9.735245 1.32 0.186 -6.248268 32.03078 ------------------------------------------------------------------------------
test simple comparison 1 and 2 vs. 3.
lincom _Icollcat_3+ 92.23*_Ico3Xme
( 1) _Icollcat_3 + 92.23 _IcolXmeals_3 = 0.0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | 46.8836 10.87319 4.31 0.000 25.50688 68.26033 ------------------------------------------------------------------------------
7. interaction comparisoin
We can compare the size of the effect of collcat at one level of meals to the size of the effect of collcat at another level of meals.
test whether 1 vs 2 effect at comparing mean to mean-1sd
lincom (_Icollcat_2+ 60.315*_Ico2Xme) - (_Icollcat_2+ 28.403*_Ico2Xme)
( 1) 31.912 _IcolXmeals_2 = 0.0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | .8983417 7.100466 0.13 0.899 -13.0612 14.85788 ------------------------------------------------------------------------------
same as
lincom 31.912 * _Ico2Xme
( 1) 31.912 _Ico2Xme = 0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | .8983401 7.100466 0.13 0.899 -13.0612 14.85788 ------------------------------------------------------------------------------
notice is the same as below after rounding error.
display 12.89125-11.99283
.89842
test whether 1 and 2 vs 3 effect at comparing mean-1sd to mean
lincom (_Icollcat_3+ 60.315*_Ico3Xme) - (_Icollcat_3 + 28.403*_Ico3Xme)
( 1) 31.912 _Ico3Xme = 0.0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | 25.36656 7.416888 3.42 0.001 10.78494 39.94819 ------------------------------------------------------------------------------
same as
lincom 31.915 * _Ico3Xme
( 1) 31.915 _Ico3Xme = 0.0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | 25.36895 7.417585 3.42 0.001 10.78595 39.95194 ------------------------------------------------------------------------------
notice is the same as
display 46.8836 - 21.51465
25.36895
8. More on predicted values
show how to get predicted values, also known as adjusted means in ancova terminology. get predicted values for group 1, 2, 3 when meals=21
lincom _cons + 21*meals + -.5*_Icollcat_2 + -.333333*_Icollcat_3 + /// (21*-.5)*_Ico2Xme + (21*-.33333)*_Ico3Xme
( 1) - .5 _Icollcat_2 - .333333 _Icollcat_3 + 21.0 meals - 10.5 _Ico2Xme - 6.99993 _Ico3Xme + _cons = 0.0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | 799.2263 9.275135 86.17 0.000 780.9914 817.4613 ------------------------------------------------------------------------------
lincom _cons + 21*meals + .5*_Icollcat_2 + -.333333*_Icollcat_3 + /// (21* .5)*_Ico2Xme + (21*-.33333)*_Ico3Xme ( 1) .5 _Icollcat_2 - .333333 _Icollcat_3 + 21.0 meals + 10.5 _IcolXmeals_2 - 6.99993 _IcolXmeals_3 + _cons = 0.0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | 810.1124 8.084814 100.20 0.000 794.2177 826.0072 ------------------------------------------------------------------------------
. lincom _cons + 21*meals + 0*_Icollcat_2 + .666667*_Icollcat_3 + /// (21* 0)*_Ico2Xme + (21* .66667)*_Ico3Xme
( 1) .666667 _Icollcat_3 + 21.0 meals + 14.00007 _Ico3Xme + _cons = 0.0 ------------------------------------------------------------------------------ api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | 794.9329 8.152465 97.51 0.000 778.9051 810.9607 ------------------------------------------------------------------------------
in case we don't trust our computations, use predict command to verify that we have gotten the correct predicted values. use the predict command and then look at predicted values when meals is 21 for each level of collcat. This works because we checked to see that we really do have meals=21 in our data file for each level of collcat.
predict pred
(option xb assumed; fitted values)
list meals collcat _Icollcat_2 _Icollcat_3 pred if meals==21
meals collcat _Icollca~2 _Icollca~3 pred 30. 21 1 -.5 -.33333333 799.2263 179. 21 2 .5 -.33333333 810.1124 208. 21 2 .5 -.33333333 810.1124 338. 21 3 0 .66666667 794.9329 377. 21 3 0 .66666667 794.9329
log close
Source: https://stats.oarc.ucla.edu/stata/webbooks/reg/chapter7/regressionwith-statachapter-7-more-on-interactions-of-categorical-and-continuous-variables/
0 Response to "Stata Create Categorical Variable From Continuous"
Post a Comment